The math games surrounding us
The cheerful statues of the Zaat Herremenieke are connected to hundreds of mathematicians worldwide, who work in a field called game theory.
Biological applications
“Over the course of my career, I became more and more captivated by biological applications. A bee doesn’t know how much nectar is in a flower, for example, or how many other bees are flying around. Nature doesn’t choose its strategy based on numbers.”
Thuijsman has since expanded the range of games he and his team analyse to include players such as foraging bees, competing cancer cells and countries fighting pollution. “The challenge is that for the type of applications we work on, there are not many tools available yet. Most models are a big abstraction of reality. If you were to make it more realistic, you need information you don’t have or include equations which cannot be solved.”
The interplay between simplicity and complexity is also what Thuijsman enjoys most. “Writing down a game can be done with very simple mathematical tools. But solving it?” His eyes light up again. “That can be incredibly complex.”
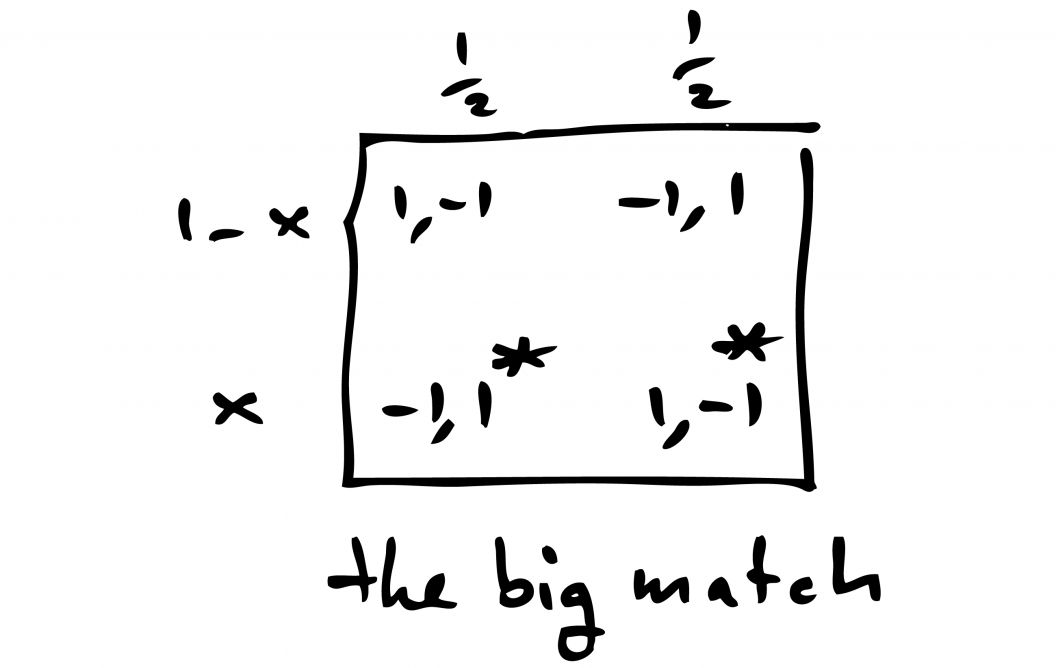
“Simple” gamesThis matrix – the numbers in the box – shows a deceptively simple game. It’s a game between two players, the row player and the column player. Both have two choices, top/bottom for the row player and left/right for the column player. The row player tries to match their opponent’s choice: she wants to choose ‘top’ if the column player chooses ‘left’ and ‘bottom’ if the column player chooses ‘right’. If the row player makes the right prediction she gets €1 from the column player, but if the row player makes the wrong guess she has to pay her opponent €1. Each player wants to win as much money as possible on average, assuming they play this game once a day until the end of time. This wouldn’t be complicated if it weren’t for those asterisks in the bottom row. “Without the asterisks, each player can simply toss a coin and have a 50% chance of winning. On average, no one loses or gains any money,” says Thuijsman. “Those asterisks mean that as soon as the row player picks the second row, the game stops. They no longer play, but the payoff of that particular day will be the payoff on all future days. If the row player gets it wrong and chooses ‘bottom’ while the column player chooses ‘left’, from then on she has to pay €1 every day.” This becomes very dangerous for the row player: if she flips a coin to make a decision, eventually the decision will be ‘bottom’. The column player can counteract that strategy by always choosing ‘left’, so that once the game is locked in, her opponent forever gets money from the row player. It took game theorists 11 years to come up with a favourable strategy for the row player. There is a way for her to lose at most -€0.001, by carefully monitoring the choices of her opponent. |
‘t Zaat Herremenieke
’t Zaat Herremenieke represents a band of five street musicians dressed up in carnival attire.
Such groups traditionally gather at Vrijthof square during the city’s annual carnival.
Upon their installation in 1993, the bronze statues were monochromatic. Artist Han van Wetering seized the opportunity to give them the bright colours they have today when they were temporarily removed during the renovation of Vrijthof square in 2004.
’t Zaat Herremenieke
Vrijthof square
6211 LC Maastricht