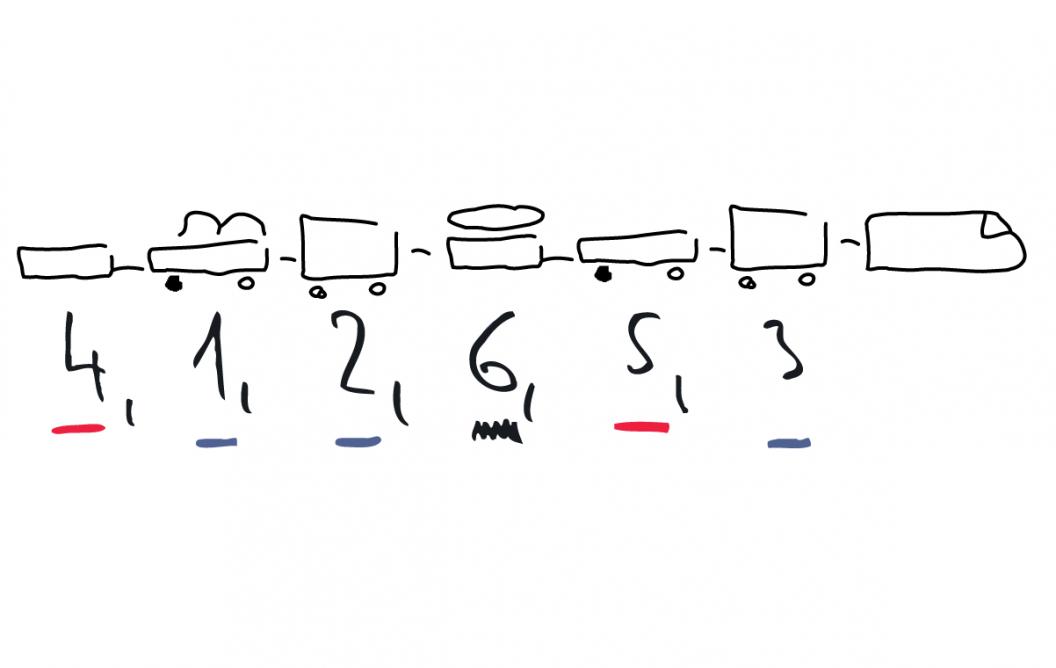Advanced problem solving
Did you ever stop to think whether you solved a puzzle in the most efficient way possible? Math is here to help, and you may want to pay special attention if you marshal trains for a living.

Logistic puzzles of the future
The problem – or puzzle – he currently works on is quite different from a mathematical point of view, but it still lies in the area of logistics.
“I currently focus on package delivery by electric vehicles. They have a limited range because of their batteries. If you have packages that need to travel longer distances, you cannot do it with a single vehicle. I’m trying to understand how to do it in a collaborative way. Which routes should which vehicles take, where do they transfer the packages between each other, in which order do they go? You can optimize it in many ways: minimize the energy used, the total distance travelled, or the time it takes for delivery. Again, it’s not about whether you can do it manually, but about whether we can design an algorithm that solves it for any such situation.”
Shunting for dummies
|
In shunting yards, a train with decoupled wagons backs up and propels one or multipe rear wagons into the yard (either by generating enough momentum or by pushing it over a small hill, allowing gravity to take over). Switches then steer the wagons into one of the yard’s parallel tracks, so they can be retrieved and re-coupled in a different order. What is the minimum amount of steps – the amount of times a train needs to back up and propel wagons – required to separate the wagons of the train in the drawing, so they can be re-combined in the order 1-6? If needed, you can propel multiple wagons in one go. You can also park them on a track you already parked a previously shunted wagon on. Try for yourself, but here is a hint: it is mathematically proven that an important part of the optimal solution it is to read the sequence from left to right and identify successive numbers. Red lines mark the first consecutive read, blue the second and the black squiggle the third and last. For such a small train, it’s easy to figure out manually, but real-life shunting tends to be far more complex. |
One solution to accommodate them all
It is that goal which separates the mathematician from the end user. “If I have an algorithm which is good, the industry is happy, but they are not interested in the proof itself. The proof is nice, it’s long or short, no one cares as long it works. For me, I’m not satisfied knowing something is just good. I want to know how it behaves.”
Noorderbrug and the railway station area
Maastricht railway station
Stationsplein 29
6221 BT Maastricht