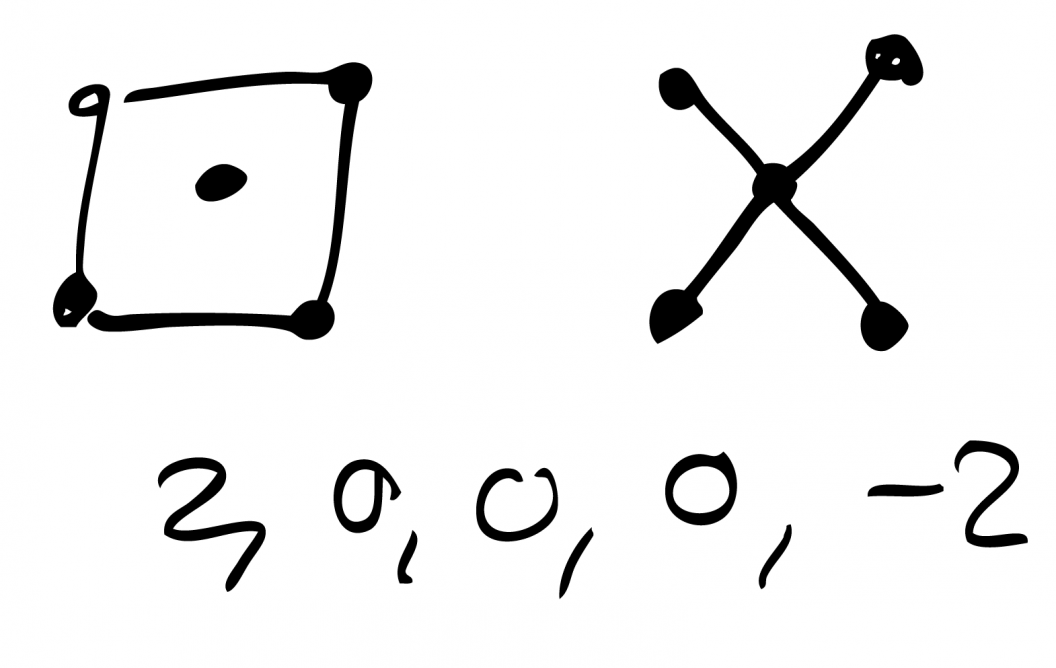A unique Dutch windmill
As it turns out, Dutch windmills are not just national icons. They also hold a unique position in the mathematical landscape.
Partial ID
Although eigenvalues don’t hold all the keys, they do contain important structural information about the graph they represent. For example, the number of eigenvalues corresponds to the number of nodes. Eigenvalues can also reveal the number of triangular shapes made by lines in the graph. But what else can they tell us?
Well, that’s what Abiad is trying to figure out. “At the moment, I’m developing techniques to construct graphs that share the same eigenvalues, and I ask the reverse question: which properties of the graphs are not identifiable from their eigenvalues?”
Different graphs, same eigenvaluesWhile the two graphs in this picture share some features, such as containing five nodes, they are clearly different. The center node of the left graph has no connections, while the center node of the right graph is connected to every other node. However, their eigenvalues - the row of numbers on the bottom - are the same. |
Mathematical landmarks
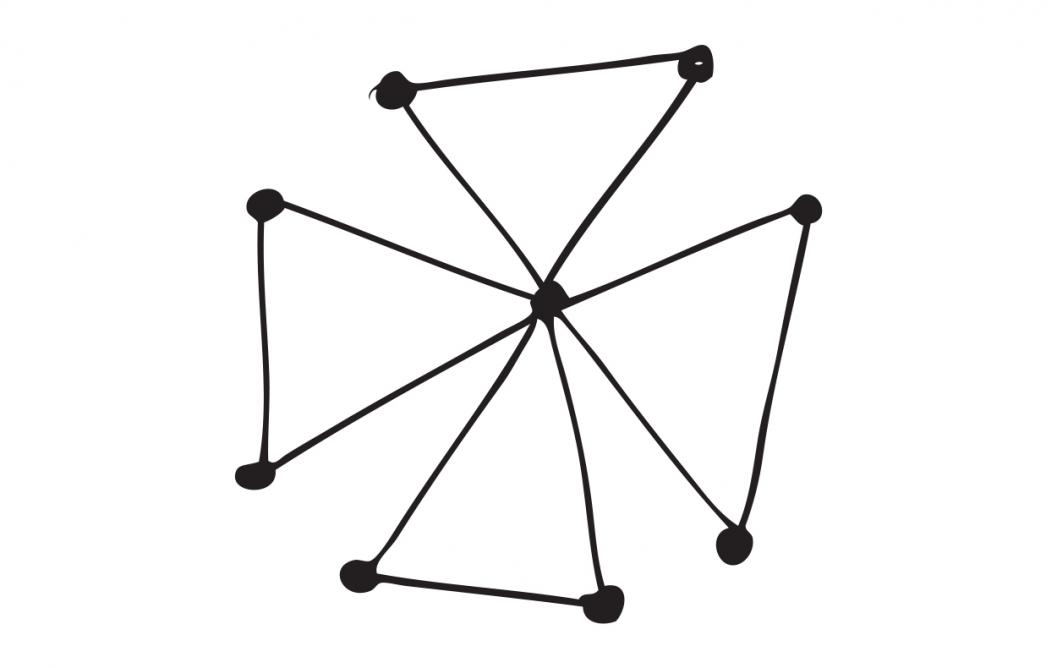
So far so good – back to the windmill. Abiad: “Dutch windmills have their own graph. It’s obvious to see why the graph has that name. But this graph is actually quite special, since it is completely recognizable* from its eigenvalues alone.”
“It is usually difficult to prove that eigenvalues uniquely identify a graph, because you have to exclude every other graph you can imagine. You can ask: which graphs can be characterized by their eigenvalues? This question is the main focus of my research. The answer is still largely unknown.”
Indeed: easy to grasp, hard to solve. And what about the longing for creativity that made Abiad switch to mathematics? “The proof is different for each graph family. There are no clear recipes for proofs. It can also be hard to see how to solve a problem, although the answer may be relatively simple. Yes,” she smiles, “I find mathematics extremely challenging and intensely creative.”
* …Except when the number of sails equals sixteen, somehow.
The Dutch windmill graphThe Dutch windmill graph is alternatively called the Friendship graph. The graph on the left has four sails, although Friendship graphs can have different numbers of sails too. You could see this graph as an abstract network representing four couples who don’t know each other, and who all have the same mutual friend: the center node. The associated Friendship theorem from the 1960s proved that if there is a group of people in which every pair has one friend in common, then one person must be a friend of everyone in the group. |
The Torenmolen van Gronsveld (tower mill of Gronsveld)
This 17th century mill is the southernmost windmill in the Netherlands. It is one of four tower mills remaining in the country: round, vertical windmills constructed from brick.
They grind grain and only the top can rotate 360 degrees for the fans to catch the wind.
Within the four remaining tower mills, the Torenmolen van Gronsveld is the only mill with the mechanism that rotates the top placed on the outside of the tower.
The Torenmolen van Gronsveld still operates, albeit on a voluntary basis, and it is listed in the top 100 of Dutch national monuments. Every first and third Saturday of the month, the mill is open to visitors.
Torenmolen van Gronsveld
Rijksweg 90
6228 XZ Maastricht