Running up that hill…
…with no problems? Hill climbing isn’t straightforward, whether that is for someone taking on a snowy mountain or for a computer trying to find solutions in an abstract space.

Man vs Machine climbing
“What a hill climbing algorithm does: it starts in a random place, looks at the performance of solutions directly around it and moves a little in the direction of the largest improvement. Once there, it starts over. What is the steepest way up from my new position? When it reaches a local peak – a solution where there are no better solutions directly around it – the algorithm stops.”
Hill climbing does not guarantee finding the absolute best outcome. “It’s about finding the best steps along a path to a local optimum, instead of finding the best solution. That makes it a greedy approach,” says Driessens. “You don’t consider all solutions. It’s like looking at the tallest hill we can see from here, but that doesn’t exclude a higher one lying right around the corner.”
Luckily for him, this particular hill seems to do just fine. Is it a nice day for a walk in the hills? The jury is out on that one, but for sleighing, it must’ve been perfect. After his first involuntary slide down the mountain, a widely grinning Driessens gives it a second go before returning to his office downtown.
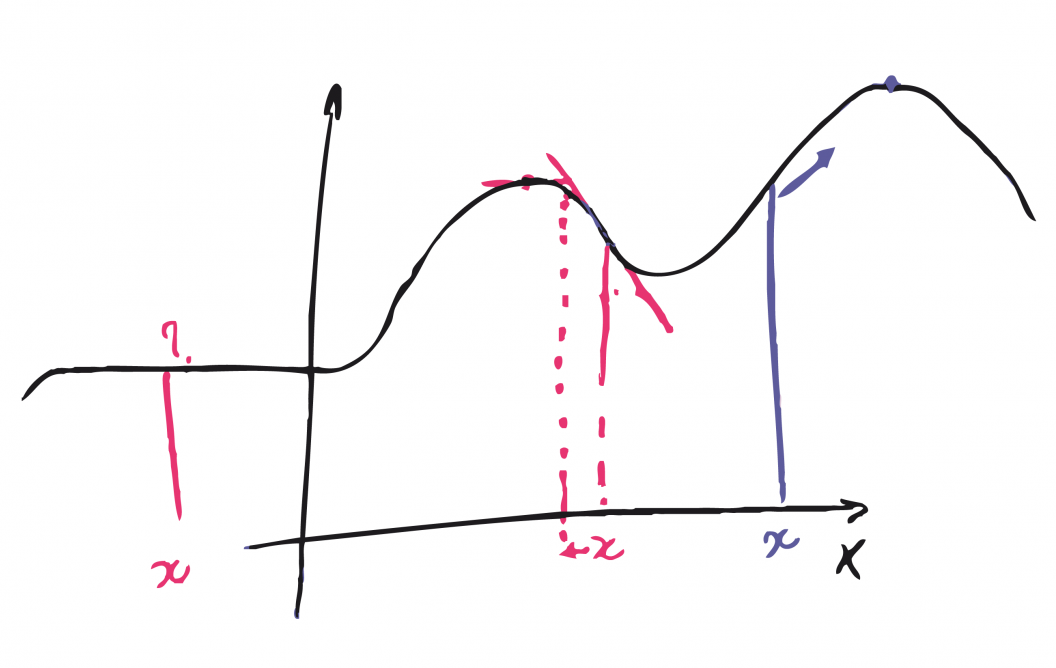
Hill climbing, the mathematicsConsider this curve, representing an abstract performance landscape. It has two peaks, or optima, representing relatively good solutions. A hill climbing algorithm starts in a random place and then calculates which way it should move to achieve the largest improvement. If the algorithm starts at the position marked by the middle red x, it moves to the left until it finds the first peak. If the algorithm starts at the blue x, the steepest increase steers it towards the right until it finds a different peak than the red starting position did. Finally, if the algorithm starts at the position marked by the leftmost red x, it won’t move, since there is no slope surrounding it. It’s a poor starting position, but the same mechanism of not moving when there is no slope allows the algorithm to stop when it does reach a peak. To get an idea of all or the highest peaks in the landscape, the algorithm should be run multiple times with different starting positions. Mathematically, hill climbing means looking at the so-called gradient. “It’s a nice word for the derivative of the function,” says Driessens, “in multiple dimensions. You go one step sideways, and then see how many steps you go up or down. This curve shows one dimension. The maximum number of dimensions I can draw is two, but these algorithms deal with literally millions of dimensions.” |
Fort St. Pieter
Luikerweg 71
6212 NH Maastricht