Docentendag Wiskunde - tussen eindig en overaftelbaar

Kom naar de docentendag Wiskunde

Datum: 9 December 2025

Locatie: ROER College Schöndeln,  Heinsbergerweg 184, 6045 CK Roermond

Programma:
14.00 Inloop
14.30 Start masterclass
16.15 Pauze
16.30 Introductie Vaksteunpunt en ophalen behoeften
17.15 Borrel
18.00 Einde

Tijdens deze middag zal Stefan Maubach een inspirerende masterclass verzorgen:

tussen eindig en overaftelbaar  

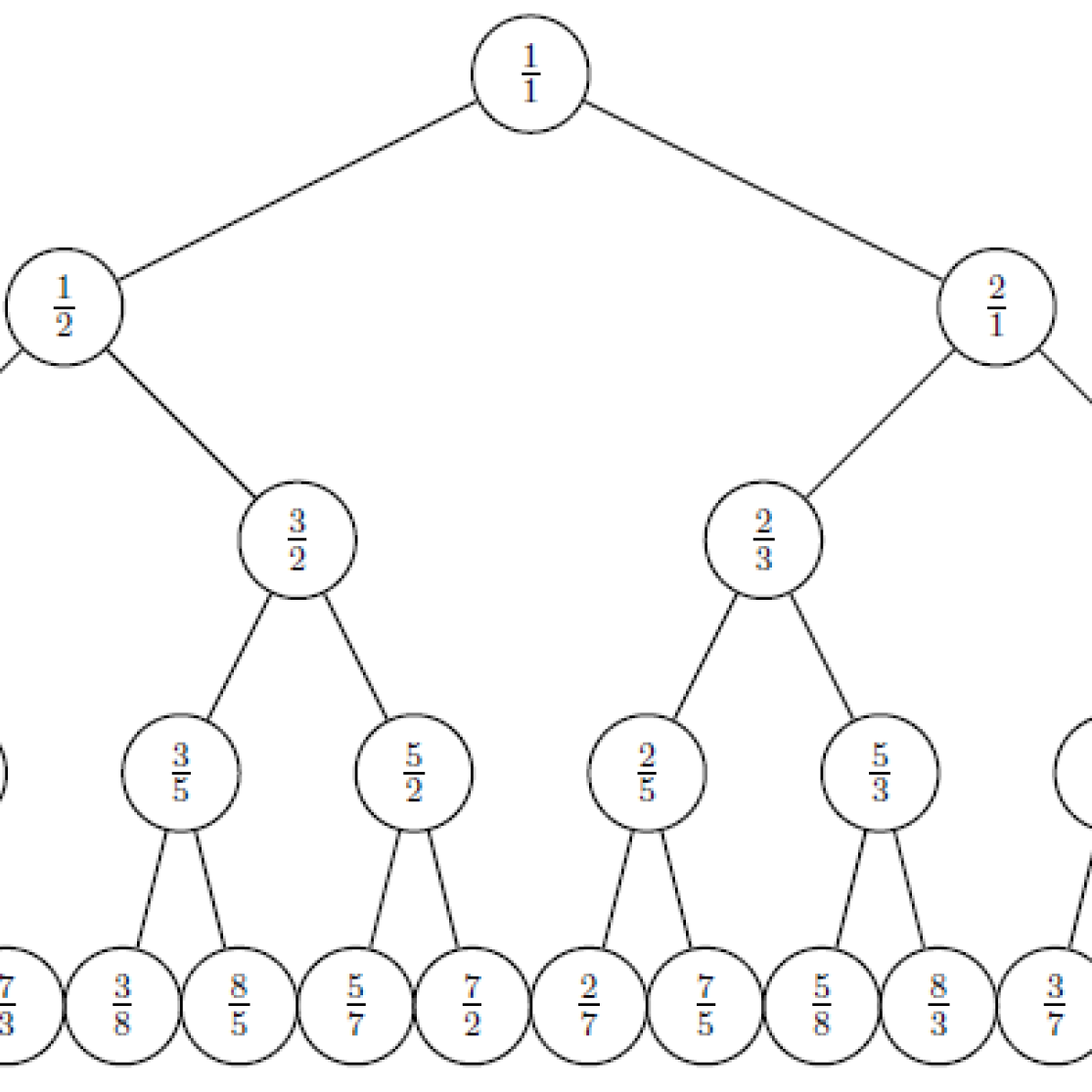
Je weet misschien nog dat Q aftelbaar is, er bestaat een bijectie N—> Q. Echter, je hebt bijna zeker geen expliciete formule hiervoor gezien. Als dit feitje bewezen wordt, dan is dat praktisch altijd via een argument dat aantoont dat die bijectie bestaat, maar hoe hij er precies uitziet, en waar bijvoorbeeld 37 op afgebeeld wordt, weet je niet. Dat is precies wat we gaan doen, we gaan een expliciete formule geven van een bijectie N—> Q en we gaan genieten van de kleine bewijsjes die we moeten doen om dit voor elkaar te krijgen. En wat heeft die te maken met de Calkin-Wilf boom?

Vervolgens presenteren we de laatste ontwikkelingen rond het Vaksteunpunt Wiskunde. De Universiteit Maastricht en de Technische Universiteit Eindhoven werken samen aan vaksteunpunten voor ieder schoolvak te beginnen met de STEM-vakken. Het Vaksteunpunt Wiskunde wordt het eerste in deze serie.

Doel van de vaksteunpunten is onder andere het verbeteren van de aansluiting tussen VO en HO. De activiteiten van het steunpunt zijn altijd vraag gedreven. Dit geeft jullie de kans input te leveren. Denk bijvoorbeeld aan onderwerpen als de aanstaande curriculumherzieningen, verrijking van bestaande lessen, ontwikkelingen in onderzoek, enz.

Natuurlijk sluiten we af met een netwerkborrel.

Meld je nu aan!

Deel deze uitnodiging met zoveel mogelijk collega’s!